Adversarial Search in Artificial Intelligence (AI)

In this page, we will learn about Adversarial Search in Artificial Intelligence (AI), Adversarial Search, Zero-Sum Game, Zero-sum game: Embedded thinking, Formalization of the problem, Game tree, and Example Explanation of Game tree.

---

Adversarial Search

Adversarial search is a type of search in which we look at the problem that develops when we try to plan ahead of the world while other agents plan against us.

• We've looked at search methods that are solely linked with a single agent that attempts to find a solution, which is commonly stated as a series of actions, in prior subjects.
• However, there may be times when more than one agent is searching for the same answer in the same search space, which is common in game play.
• The environment with more than one agent is referred to as a multi-agent environment, in which each agent is an adversary to the other and competes against them. Each agent must consider the actions of other agents as well as the consequences of their actions. Each agent have to consider the action of the other agent and effect of that action on their performance.
• Adverbial searches, often known as Games, are searches in which two or more players with opposing aims try to explore the same search space for a solution.
• Games are modeled as a Search problem and a heuristic evaluation function, which are the two primary variables that aid in the modeling and solving of games in AI.

• Perfect information: A game with perfect information is one in which agents have entire access to the board. Agents have access to all game information and can watch each other's movements. Chess, Checkers, Go, and other games are examples.
• Imperfect information: Games with imperfect information are those in which the agents do not have all of the information about the game and are unaware of what is going on, such as tic-tac-toe, Battleship, blind, Bridge, and so on.
• Deterministic games: Deterministic games are ones that follow a rigid pattern and set of rules, with no element of chance. Chess, Checkers, Go, tic-tac-toe, and other games are examples.
• Non-deterministic games: Non-deterministic games are those that have a variable number of unpredictable events and a chance or luck aspect. Dice or cards are used to introduce the element of chance or luck. These are unpredictably generated, and each action reaction is unique. Stochastic games are another name for such games. Backgammon, Monopoly, Poker, and other games are examples.

Note: In this topic we'll talk about deterministic games, fully observable environments, zero-sum games, and where each agent acts alternately.

Zero-Sum Game

• Zero-sum games are adversarial searches in which there is only one winner.
• Each agent's gain or loss of utility in a zero-sum game is exactly balanced by the losses or gains of another actor.
• One player attempts to maximize a single value, while the other attempts to minimize it.
• A ply is a single move made by one player in the game.
• Zero-sum games include chess and tic-tac-toe.

---

Zero-sum game: Embedded thinking

The Zero-sum game entails embedded reasoning, in which one agent or player attempts to determine:

• What to do. The opponent also thinks what to do
• How to decide the move
• The opponent also thinks what to do

Each player is trying to figure out how his opponent will react to his moves. To address gaming problems in AI, this necessitates embedded thinking or backward reasoning.

Formalization of the problem:

A game is a type of AI search that can be structured into the following elements:

• Initial state:This specifies how the game is set up at the beginning.
• Player (s): indicates which player(s) has moved in the state space.
• Action(s): It returns the set of allowed moves in state space as an action.
• Result(s, a): The transition model defines the outcome of moves in the state space.
• Terminal-Test(s): If the game is over, the terminal test is true; otherwise, it is false. Terminal states are the states in which the game comes to a finish.
• Utility(s, p): The final numeric value for a game that finishes in terminal states s for player p is returned by a utility function. It's also known as the payout function. Chess has three possible outcomes: win, defeat, or draw, with payoff values of +1, 0, and 12. In addition, tic-tac-toe, utility values are +1, -1, and 0.

Game tree:

A game tree is a tree in which the nodes represent game states and the edges represent player moves. Initial state, actions function, and result function are all part of the game tree.
Example: Tic-Tac-Toe game tree:

The following are some of the game's most important features of Tic-Tac-Toe game tree.

• There are two players MAX and MIN.
• Players have an alternate turn and start with MAX.
• MAX maximizes the result of the game tree
• MIN minimizes the result.

---

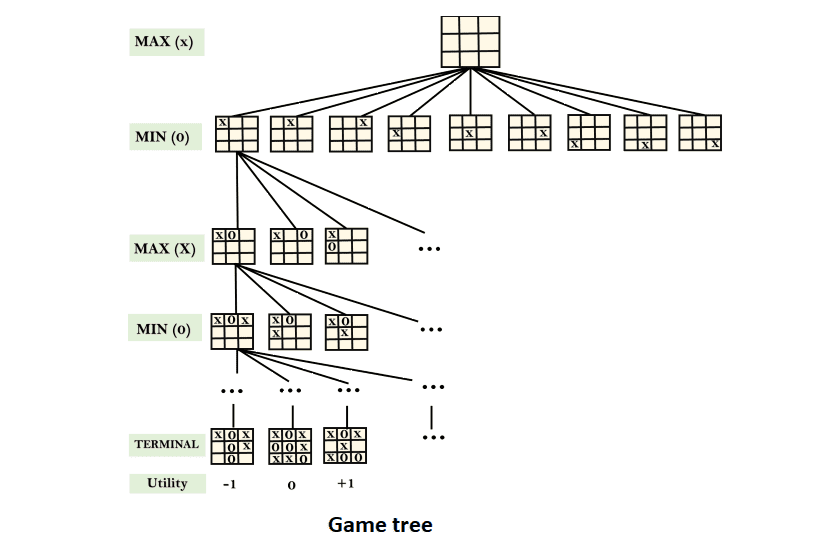
Example Explanation of Game tree:

• MAX has 9 possible moves from the start because he is the first player. Both players alternately place x and o until we reach a leaf node where one player has three in a row or all squares are filled.
• Both players will compute the best possible utility versus an optimum adversary for each node, called the minimax value.
• Assume that both players are well-versed in tic-tac-toe and are playing their best game. Each player is trying everything he can to keep the other from winning. In the game, MIN is working against Max.
• So, in the game tree, we have a Max layer, a MIN layer, and each layer is referred to as Ply. The game proceeds to the terminal node, with Max placing x and MIN placing o to prevent Max from winning.
• Either MIN or MAX wins, or the game ends in a tie. This game-tree represents the whole search space of possibilities in which MIN and MAX alternately play tic-tac-toe.

As a result, the adversarial Search for the Minimax technique is:

• It is designed to determine the best strategy for MAX to win the game.
• It employs a depth-first search strategy.
• The ideal leaf node in the game tree could appear at any level of the tree.
• Minimax values should be propagated up the tree until the terminal node is found.

The optimal strategy in a particular game tree can be determined by looking at the minimax value of each node, which can be expressed as MINIMAX (n). MAX prefers to move to a maximum value state, while MIN prefers to move to a minimum value state, so:

---