Hill Climbing Algorithm in AI

Table of Content:

• What is Hill Climbing Algorithm in AI?
• Main features of Hill Climbing Algorithm.
• State-space Diagram for Hill Climbing
• Different regions in the state space landscape
• Types of Hill Climbing Algorithm
• Simple Hill Climbing.
• Algorithm for Simple Hill Climbing
• Steepest-Ascent hill climbing.
• Algorithm for Steepest-Ascent hill climbing
• Stochastic hill climbing.
• Algorithm for Stochastic Hill Climbing
• Problems in Hill Climbing Algorithm.
• Simulated Annealing.

Content Highlight:

The Hill Climbing Algorithm is a local search technique in AI, aiming to find optimal solutions by iteratively moving towards higher values. It's like climbing a hill, with the peak representing the best solution. Features include a greedy approach and no backtracking. Problems like local maxima, plateaus, and ridges can hinder progress. Simulated Annealing addresses these issues by introducing randomness, allowing for dynamic exploration and better optimization.

What is Hill Climbing Algorithm in AI?

The Hill Climbing Algorithm in Artificial Intelligence is a local search algorithm that aims to find the optimal solution to a problem by iteratively moving towards the direction of increasing elevation or value. It is like climbing a hill to reach the peak, where the peak represents the best solution to the given problem.

The algorithm starts with an initial solution and makes incremental changes to it, always choosing the neighbor with a higher value. It continuously explores neighboring solutions, moving uphill in the search space, until it reaches a point where no immediate neighbor has a higher value. At this point, the algorithm terminates, considering the current solution as the local optimum.

Hill climbing is often used for optimization problems where the goal is to find the best possible solution based on some criteria. One classic example is the Traveling Salesman Problem, where the objective is to minimize the distance traveled by a salesman visiting a set of cities.

This algorithm is sometimes referred to as greedy local search because it makes decisions based on the immediate neighborhood without considering a global view of the entire search space. It is efficient when a good heuristic (a rule of thumb) is available to guide the search.

Features of Hill Climbing:

Some main features of Hill Climbing Algorithm are:

1. Generate and Test Variant: Hill Climbing is a variant of the Generate and Test method. In this approach, the algorithm generates potential solutions and tests them, utilizing feedback to determine the direction for further exploration in the search space.

2. Greedy Approach: Hill climbing adopts a greedy strategy, always moving in the direction that optimizes the cost or value. It focuses on immediate improvements, making decisions based on the current best available option without considering the global picture.

3. No Backtracking: Unlike some other search algorithms, Hill Climbing does not involve backtracking. It does not remember or revisit previous states in the search space. Once a decision is made and a direction is taken, the algorithm continues to move forward without retracing its steps.

These distinctive features make Hill Climbing an efficient and straightforward algorithm, particularly well-suited for scenarios where a greedy local search is appropriate and backtracking is unnecessary.

State-space Diagram for Hill Climbing:

The state-space diagram is a visual representation of the hill-climbing algorithm, depicting the relationship between various states of the algorithm and the objective function or cost. It provides a graphical insight into the exploration of the search space.

On the Y-axis of the diagram, we represent the function, which can be either an objective function or a cost function. The X-axis corresponds to the state-space, representing different states explored by the algorithm.

If the function on the Y-axis represents cost, the goal of the search is to identify both the global minimum and local minimum within the state-space. The algorithm aims to minimize the cost, moving towards states that result in lower values.

On the other hand, if the function on the Y-axis is an Objective function, the search goal is to find both the global maximum and local maximum within the state-space. In this case, the algorithm strives to maximize the objective function, seeking states that lead to higher values.

The state-space diagram visually captures the exploration and progression of the hill-climbing algorithm as it navigates through various states, aiming to reach the optimal solution based on the specified criteria.

Different regions in the state space landscape:

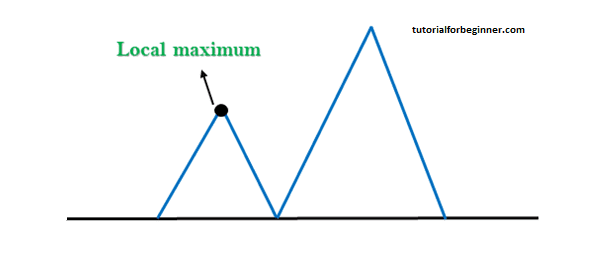
Local Maximum: A local maximum is a state in the state space landscape that is better than its neighbor states, but there exists another state with a higher value. It represents a peak within a local area.

Global Maximum: The global maximum is the best possible state in the state space landscape. It holds the highest value of the objective function and is the ultimate goal of the search.

Current State: The current state is the position of an agent in the landscape diagram at a given point in time. It represents the state the algorithm is currently exploring.

Flat Local Maximum: A flat local maximum is a region in the landscape where all the neighbor states of the current state have the same value. It is a flat, elevated area in the state space.

Shoulder: A shoulder is a plateau region in the state space landscape that has an uphill edge. It represents a flat stretch before an incline, offering a unique characteristic in the exploration of the search space.

Understanding these different regions in the state space landscape is crucial for interpreting the behavior of the algorithm as it navigates through various states during the search process.

Types of Hill Climbing Algorithm:

1. Simple hill Climbing.
2. Steepest-Ascent hill-climbing.
3. Stochastic hill Climbing.

1. Simple Hill Climbing:

Simple hill climbing is the most straightforward implementation of a hill climbing algorithm. It adopts a minimalistic approach, evaluating only one neighbor node state at a time. The algorithm selects the first neighbor that optimizes the current cost and sets it as the current state. It essentially makes a decision based on the immediate improvement without exploring further.

This algorithm has the following features:

• Less Time Consuming: Simple hill climbing is characterized by its efficiency in terms of time. It evaluates and selects the first neighbor state quickly, making it less time-consuming compared to more complex algorithms.
• Less Optimal Solution: While being efficient, simple hill climbing may yield less optimal solutions. Since it only considers the immediate neighborhood, it might miss global optima, resulting in solutions that are suboptimal.
• Solution is not Guaranteed: The algorithm does not guarantee finding the best solution. Depending on the initial state and the search space, it may converge to a local optimum without exploring the entire solution space.

Simple hill climbing is suitable for scenarios where quick decision-making is prioritized over exhaustive exploration, and where a less optimal solution is acceptable within the given constraints.

Algorithm for Simple Hill Climbing:

• Step 1: Evaluate the initial state; if it is the goal state, then return success and Stop.
• Step 2: Loop Until a solution is found or there is no new operator left to apply.
• Step 3: Select and apply an operator to the current state.
• Step 4: Check the new state:
  • If it is the goal state, then return success and quit.
  • Else if it is better than the current state, then assign the new state as the current state.
  • Else if not better than the current state, then return to Step 2.
• Step 5: Exit.

This Simple Hill Climbing algorithm starts by evaluating the initial state and continues to loop until a solution is found or there are no new operators left to apply. It selects and applies an operator to the current state, checks the new state, and decides whether to proceed based on the goal state and the quality of the new state compared to the current state. The process concludes when a solution is found or the algorithm determines that there is no better state to explore.

2. Steepest-Ascent hill climbing:

The Steepest-Ascent algorithm is a variation of the simple hill climbing algorithm. In this approach, the algorithm goes beyond the simplicity of evaluating just one neighboring node. Instead, it examines all the neighboring nodes of the current state and selects the one that is closest to the goal state.

This algorithm is characterized by the following key aspects:

• It is a variation of the simple hill climbing algorithm, introducing a more exhaustive search for neighboring nodes.
• The algorithm examines all neighboring nodes of the current state, considering a wider range of possibilities in the search space.
• The selection criterion is based on choosing the neighbor node that is closest to the goal state. This aims to achieve a more direct path towards the solution.
• Due to the comprehensive search for multiple neighbors, the Steepest-Ascent algorithm consumes more time compared to the simplicity of the basic hill climbing approach.

This method prioritizes a more exhaustive exploration of the search space by considering all available neighbors, aiming to efficiently move towards the optimal solution.

Algorithm for Steepest-Ascent hill climbing:

• Step 1: Evaluate the initial state. If it is the goal state, return success and stop; else, make the current state the initial state.
• Step 2: Loop until a solution is found or the current state does not change.
  • Let SUCC be a state such that any successor of the current state will be better than it.
  • For each operator that applies to the current state:
    • Apply the new operator and generate a new state.
    • Evaluate the new state.
    • If it is the goal state, return it and quit; else, compare it to SUCC.
    • If it is better than SUCC, set the new state as SUCC.
    • If SUCC is better than the current state, set the current state to SUCC.
• Step 3: Exit.

This Steepest-Ascent Hill Climbing algorithm iteratively explores potential solutions, evaluating each successor state to find the one that is closest to the goal state. The process continues until a solution is found or no improvement can be made.

3. Stochastic hill climbing:

Stochastic Hill Climbing is a variation of the hill climbing algorithm that introduces randomness in the decision-making process. In this approach, when exploring potential solutions, the algorithm evaluates each successor state and probabilistically decides whether to accept the move. This introduces a level of randomness in accepting uphill moves, allowing the algorithm to potentially escape local optima.

Algorithm for Stochastic hill climbing:

• Step 1: Evaluate the initial state. If it is the goal state, return success and stop; else, make the current state the initial state.
• Step 2: Loop until a solution is found or a termination condition is met.
  • For each operator that applies to the current state:
  • Apply the new operator and generate a new state.
  • Evaluate the new state.
  • If it is the goal state, return it and quit.
  • Calculate the probability of accepting the new state.
  • If the probability is greater than a randomly generated value, accept the new state; otherwise, stay in the current state.
• Step 3: Exit.

By considering a probability of accepting a move, Stochastic Hill Climbing is more flexible than deterministic approaches, offering a balance between exploration and exploitation in the search space. This randomness helps the algorithm to explore different regions of the space, potentially leading to the discovery of more diverse solutions.

Problems in Hill Climbing Algorithm:

Local Maximum: A local maximum is a peak state in the landscape that is better than each of its neighboring states, but there is another state also present which is higher than the local maximum. This situation can limit the algorithm's progress.

Solution: The backtracking technique serves as a solution for overcoming the challenge of being stuck in a local maximum. Create a list of the promising paths so that the algorithm can backtrack the search space and explore other paths as well, allowing it to break free from local optima.

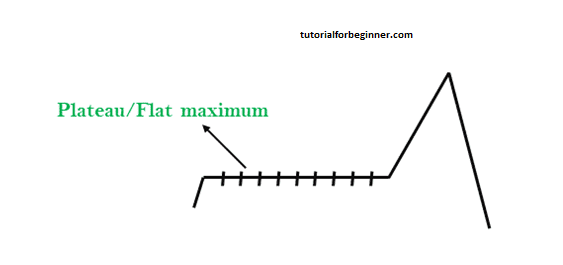
2. Plateau: A plateau is the flat area of the search space where all the neighbor states of the current state contain the same value. Due to this, the algorithm struggles to find the best direction to move, and a hill-climbing search might get lost in the plateau area.

Solution: To address the plateau issue, adjust the step size by either taking big steps or very little steps while searching. Randomly selecting a state far away from the current state can help the algorithm escape plateau regions and explore non-plateau areas.

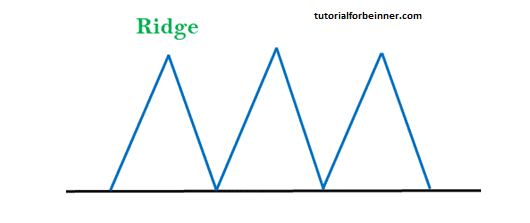
3. Ridges: A ridge is a special form of the local maximum. It has an area higher than its surrounding areas but itself has a slope and cannot be reached in a single move.

Solution: Mitigate the ridge problem by employing techniques like bidirectional search or by exploring different directions. These approaches can enhance the algorithm's ability to navigate through ridge formations.

Simulated Annealing:

Introduction: Simulated Annealing is a sophisticated optimization algorithm, addressing the limitations of traditional hill-climbing algorithms. While hill-climbing may get stuck on local maxima, and applying random walks may lead to completeness but inefficiency, Simulated Annealing strikes a balance, offering both efficiency and completeness.

Mechanical Analogy: In mechanical terms, annealing is a process of hardening a material like metal or glass by heating it to a high temperature and then gradually cooling it. This allows the material to reach a low-energy crystalline state. Simulated Annealing adopts a similar concept in the algorithmic realm.

Algorithmic Process: In Simulated Annealing, the algorithm diverges from traditional hill-climbing approaches. Instead of always making moves towards higher values, it introduces an element of randomness. If a randomly chosen move improves the current state, the algorithm follows that path. However, if the random move does not result in improvement, the algorithm may choose to follow a path with a probability of less than 1, even if it involves moving downhill, before potentially exploring another path.

This probabilistic approach allows Simulated Annealing to escape local optima and explore the solution space more dynamically, enhancing its efficiency and completeness in finding optimal solutions.