Alpha-Beta Pruning in AI

Table of Content:

Content Highlight:

The provided content offers an extensive explanation of Alpha-Beta Pruning in Artificial Intelligence (AI), detailing its significance, working mechanism, conditions, and the role of move ordering in optimizing its efficiency. It covers key concepts such as the minimax algorithm, initialization, pruning, and backtracking, along with practical examples and rules for achieving effective move ordering. Overall, it serves as a comprehensive guide to understanding and implementing Alpha-Beta Pruning in AI, highlighting its crucial role in enhancing search algorithms for strategic games.

What is Alpha-Beta Pruning in Artificial Intelligence?

Alpha-beta pruning is a game-changing optimization technique in artificial intelligence (AI) that revolutionizes game tree search algorithms. By strategically pruning unnecessary branches, alpha-beta pruning enhances the efficiency of the search process, allowing AI systems to delve deeper into the game tree and make informed decisions. Whether you're developing AI for chess, checkers, or other strategic games, mastering alpha-beta pruning is essential for achieving superior performance. Dive into the world of AI optimization and elevate your game with alpha-beta pruning expertise.

Alpha-beta pruning stands as a refined iteration of the minimax algorithm, strategically engineered to bolster its efficacy. Traditional minimax searches entail an exponential explosion of game states with each increment in tree depth. While eradicating this exponential growth entirely proves unattainable, alpha-beta pruning offers a compelling solution, curbing it significantly.

This pruning methodology revolves around two pivotal parameters: Alpha and Beta. Alpha signifies the paramount (highest-value) choice discovered thus far along the Maximizing player's path, initialized to negative infinity. Conversely, Beta epitomizes the finest (lowest-value) choice along the Minimizing player's trajectory, commencing at positive infinity.

Alpha-beta pruning isn't bound by depth limitations and possesses the ability to excise not only individual leaf nodes but entire subtrees. By tactically severing branches inconsequential to the final decision, the algorithm adeptly streamlines the search process, enhancing its efficiency.

Despite its efficiency enhancements, alpha-beta pruning guarantees the identical optimal move yielded by the standard minimax algorithm. Nevertheless, it accomplishes this outcome by discarding redundant nodes that would otherwise impede the algorithm's performance. In essence, alpha-beta pruning strikes an optimal balance between precision and swiftness, cementing its position as an indispensable optimization technique within game-playing AI systems.

How Alpha-Beta Pruning works:

Alpha-beta pruning works by intelligently pruning branches of the game tree that are determined to be irrelevant to the final decision, thereby reducing the number of nodes that need to be evaluated during the search process. This pruning technique is based on the concept of maintaining two threshold parameters, Alpha and Beta, which represent the minimum score that the maximizing player is assured of and the maximum score that the minimizing player is assured of, respectively.

Here's how alpha-beta pruning works step by step:

  1. Initialization: At the beginning of the search, the initial values of Alpha and Beta are set to negative and positive infinity, respectively.
  2. Search: The algorithm traverses the game tree recursively, alternating between maximizing and minimizing players. As it traverses, it updates the values of Alpha and Beta based on the scores encountered along each path.
  3. Pruning: During the search, whenever the algorithm encounters a node where the score is guaranteed to be worse than the current Alpha value (for a maximizing player) or better than the current Beta value (for a minimizing player), it prunes the subtree rooted at that node. This is because the current player would not choose that path, as it leads to a worse outcome than already known. Pruning prevents further exploration of those branches, effectively reducing the search space.
  4. Backtracking: After evaluating a node and potentially pruning its subtree, the algorithm backtracks to the parent node and continues the search with updated Alpha and Beta values.
  5. Termination: The search continues until it reaches terminal nodes (e.g., game states where a win, loss, or draw is reached) or until a certain depth limit is reached.
  6. Result: The algorithm returns the best move found based on the scores encountered during the search, which is the same as the result obtained by the standard minimax algorithm.

By strategically pruning branches that are unlikely to lead to the optimal decision, alpha-beta pruning significantly reduces the number of nodes that need to be evaluated, leading to a more efficient search process. This allows AI systems to search deeper into the game tree within a reasonable amount of time, making it a crucial optimization technique for building game-playing AI systems.

Condition for Alpha-beta pruning:

The main condition which required for alpha-beta pruning is: 


   α >= β
\

Key points about alpha-beta pruning:

  • The Max player updates the value of alpha during the search process.
  • The Min player updates the value of beta during the search process.
  • During backtracking, the node values are passed to upper nodes instead of the values of alpha and beta.
  • Only the alpha and beta values are passed to the child nodes during the search.

Pseudo-code for Alpha-beta Pruning:

 
    function minimax(node, depth, alpha, beta, maximizingPlayer) is  
    if depth == 0 or node is a terminal node then  
        return static evaluation of node  
  
    if maximizingPlayer then      // for MaximizingPlayer  
        maxEva = -infinity            
        for each child of node do  
            eva = minimax(child, depth - 1, alpha, beta, False)  
            maxEva = max(maxEva, eva)   
            alpha = max(alpha, maxEva)      
            if beta <= alpha then  
                break  
        return maxEva  
    
    else                         // for MinimizingPlayer  
        minEva = +infinity   
        for each child of node do  
            eva = minimax(child, depth - 1, alpha, beta, True)  
            minEva = min(minEva, eva)   
            beta = min(beta, minEva)  
            if beta <= alpha then  
                break          
        return minEva

Working of Alpha-Beta Pruning:

To better understand how Alpha-beta pruning works, consider a two-player search tree.
Step 1: The Max player will begin by moving from node A, where = - and = +, and passing these values of alpha and beta to node B, where again = - and = +, and Node B passing the same value to its offspring D.

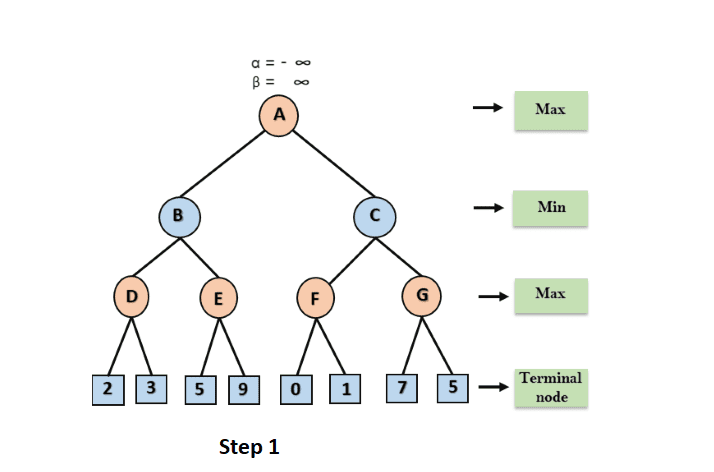
Alpha Beta Pruning step 1 in Artificial Intelligence (AI)

Step 2: The value of will be determined as Max's turn at Node D. The value of is compared to 2, then 3, and the value of at node D will be max (2, 3) = 3, and the node value will also be 3.

Step 3: The algorithm now returns to node B, where the value of will change as this is a turn of Min, now = +, and will compare with the value of the available subsequent nodes, i.e. min (, 3) = 3, so at node B now = -, and= 3.

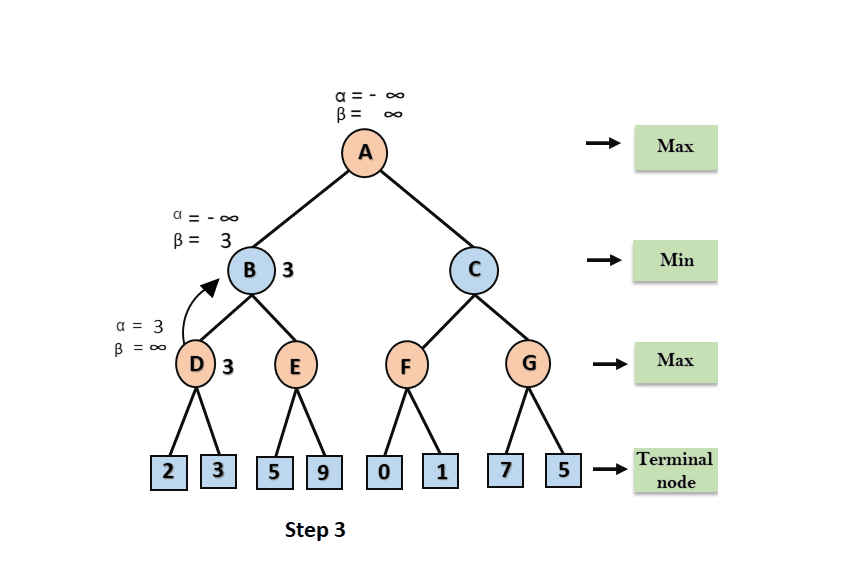
Alpha Beta Pruning step 3 in Artificial Intelligence (AI)

In the next step, algorithm traverse the next successor of Node B which is node E, and the values of α= -∞, and β= 3 will also be passed.

Step 4: Max will take its turn at node E, changing the value of alpha. The current value of alpha will be compared to 5, resulting in max (-, 5) = 5, and at node E= 5 and= 3, where >=, the right successor of E will be pruned, and the algorithm will not traverse it, and the value at node E will be 5.

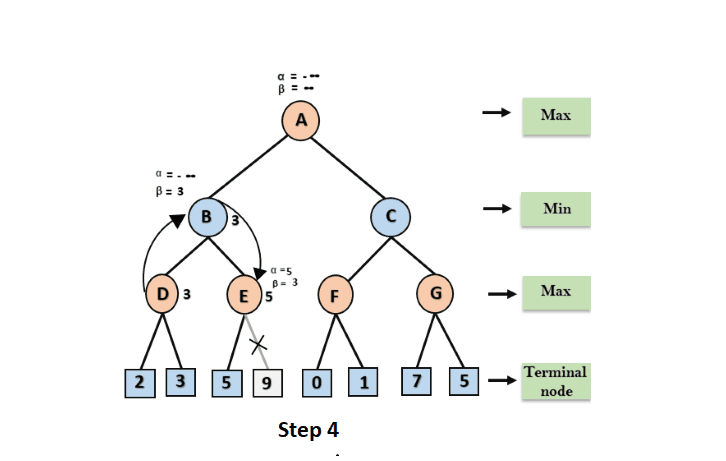
Alpha Beta Pruning step 4 in Artificial Intelligence (AI)

Step 5: The method now goes backwards in the tree, from node B to node A. The value of alpha will be modified at node A, and the highest available value will be 3 as max (-, 3)= 3, and = +. These two values will now transfer to A's right successor, Node C.

=3 and = + will be passed on to node F at node C, and the same values will be passed on to node F.

Step 6: TAt node F, the value of will be compared with the left child, which is 0, and max(3,0)= 3, and then with the right child, which is 1, and max(3,1)= 3 will remain the same, but the node value of F will change to 1.

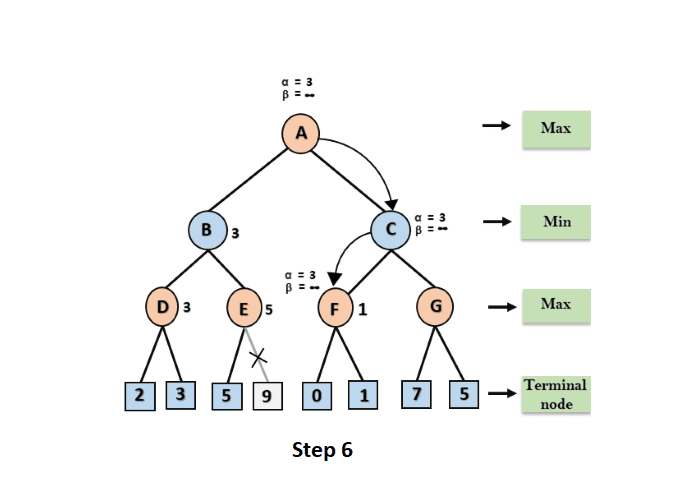
Alpha Beta Pruning step 6 in Artificial Intelligence (AI)

Step 7: Node F returns the node value 1 to node C, at C = 3 and = +, the value of beta is modified, and it is compared to 1, resulting in min (, 1) = 1. Now, at C, =3 and = 1, and again, it meets the condition >=, the algorithm will prune the next child of C, which is G, and will not compute the complete sub-tree G.

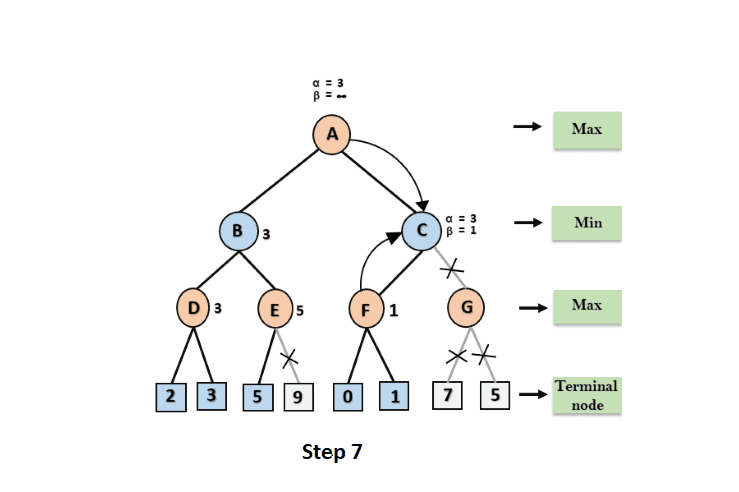
Alpha Beta Pruning step 7 in Artificial Intelligence (AI)

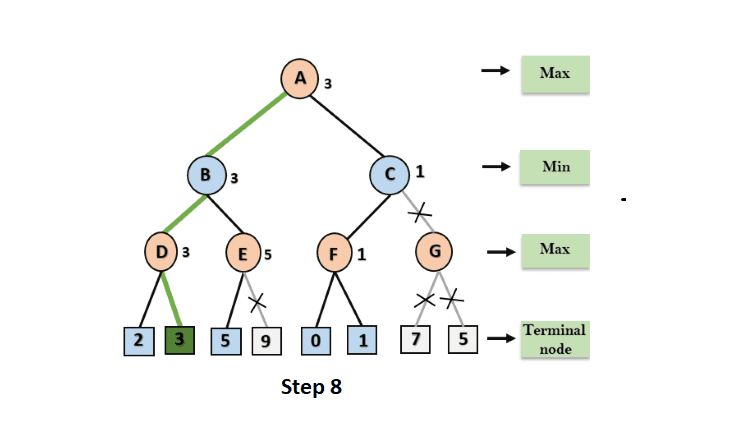
Step 8: C now returns 1 to A, with max (3, 1) = 3 being the greatest result for A. The completed game tree, which shows calculated and uncomputed nodes, is shown below. As a result, in this case, the best maximizer value is 3.

Alpha Beta Pruning step 8 in Artificial Intelligence (AI)

Move Ordering in Alpha-Beta pruning:

The effectiveness of alpha-beta pruning is highly dependent on the order in which each node is examined. Move order is a critical aspect of alpha-beta pruning

It can be categorized into two types:

  • Worst ordering: In some cases, the alpha-beta pruning algorithm does not prune any of the leaves of the tree and operates identically to the minimax algorithm. This scenario, known as worst ordering, consumes more time due to alpha-beta factors. Typically, the best move occurs on the right side of the tree. The time complexity for such an order is O(bm).
  • Ideal ordering: The ideal ordering for alpha-beta pruning occurs when significant pruning takes place in the tree, and the best moves are found on the left side of the tree. Utilizing a Depth-First Search (DFS) approach, it explores the left side of the tree first, allowing for deeper exploration in the same time frame as the minimax algorithm. The complexity in ideal ordering is O(bm/2).

Rules to find good ordering:

  • Occur the best move from the shallowest node.
  • Order the nodes in the tree such that the best nodes are checked first.
  • Utilize domain knowledge while finding the best move. For example, in Chess, prioritize moves such as captures, threats, forward moves, and backward moves.
  • Bookkeep the states, as there is a possibility that states may repeat.

Problems of Alpha-Beta pruning?

  • Overhead: Alpha-beta pruning can introduce additional overhead due to the need to maintain and update alpha and beta values during the search process.
  • Memory Consumption: Storing alpha and beta values for each node in the tree can increase memory consumption, especially for deep or large game trees.
  • Implementation Complexity: Implementing alpha-beta pruning correctly requires careful consideration of the algorithm's logic and handling of edge cases, leading to increased implementation complexity.
  • Optimality Concerns: While alpha-beta pruning can significantly reduce the search space, there is no guarantee that it will always find the optimal solution, especially in cases where the heuristic evaluation function is not accurate.
  • Ordering Dependency: The effectiveness of alpha-beta pruning is highly dependent on the ordering of moves, which can be challenging to optimize in practice.