Search Algorithms in AI

Table of Content:

Content Highlight:

Introduction: AI relies on search algorithms for problem-solving.

Problem-solving agents: Rational agents in AI use search strategies for problem-solving.

Search Algorithm Terminologies: Key terms include search, search space, start state, goal test, search tree, actions, transition model, path cost, solution, and optimal solution.

Properties of Search Algorithms: Completeness ensures solution return, optimality guarantees the best solution, time complexity measures efficiency, and space complexity assesses storage requirements.

Types of Search Algorithms: Uninformed (Blind) and Informed (Heuristic) searches.

Informed Search: Informed search leverages domain knowledge for efficient problem-solving.

Greedy Search and A* Search: Examples of informed search algorithms optimizing with domain knowledge.

Introduction:

Search algorithms stand as the backbone of Artificial Intelligence (AI), serving as indispensable tools for problem-solving agents. In this comprehensive guide, we'll delve into the intricacies of search algorithms, exploring their pivotal role in enabling rational agents to navigate complex problem spaces and achieve optimal outcomes.

Problem-solving agents:

Search techniques serve as universal problem-solving methods within the realm of Artificial Intelligence (AI). Rational agents, also known as problem-solving agents, extensively rely on specialized search strategies and algorithms to address specific problems and deliver optimal results. These goal-based agents utilize atomic representation in their analytical processes. Throughout this exploration, we will delve into a diverse range of problem-solving search algorithms, uncovering the methodologies that empower agents to navigate complex scenarios and achieve superior outcomes.

Search Algorithm Terminologies:

  • Search: Search is a systematic step-by-step procedure designed to solve a search problem within a specified search space.
  • Search Problem Factors: A search problem involves three key factors:
    • Search Space: Represents a set of potential solutions within the system.
    • Start State: The initial state from which the agent commences its search.
    • Goal Test: A function observing the current state and determining whether the goal state is achieved.
  • Search Tree: A tree representation of the search problem, with the root node corresponding to the initial state.
  • Actions: Descriptions of all available actions that the agent can take.
  • Transition Model: A model describing the effects of each action, often represented as a transition model.
  • Path Cost: A function assigning numeric costs to each path within the search space.
  • Solution: An action sequence leading from the start node to the goal node.
  • Optimal Solution: A solution with the lowest cost among all available solutions.

Properties of Search Algorithms:

The four most important properties of search algorithms to compare their efficiency are as follows:

Completeness: A search algorithm is deemed complete if it ensures the return of a solution whenever any solution exists for a given random input. This property signifies the algorithm's thorough exploration of the solution space to find a valid answer.

Optimality: When an algorithm discovers a solution that stands out as the best solution, boasting the lowest path cost among all alternatives, it attains the status of an optimal solution. This property underscores the algorithm's efficiency in identifying the most favorable outcome.

Time Complexity: Time complexity serves as a metric to gauge the duration an algorithm takes to complete its task. It quantifies the efficiency of the algorithm in terms of the computational time required for execution.

Space Complexity: Space complexity relates to the maximum storage space required at any point during the search. It reflects the algorithm's ability to manage and allocate memory resources effectively, considering the intricacies of the problem at hand.

Types of search algorithms:

We can divide search algorithms into uninformed (Blind search) and informed (Heuristic search) algorithms based on the search difficulties.

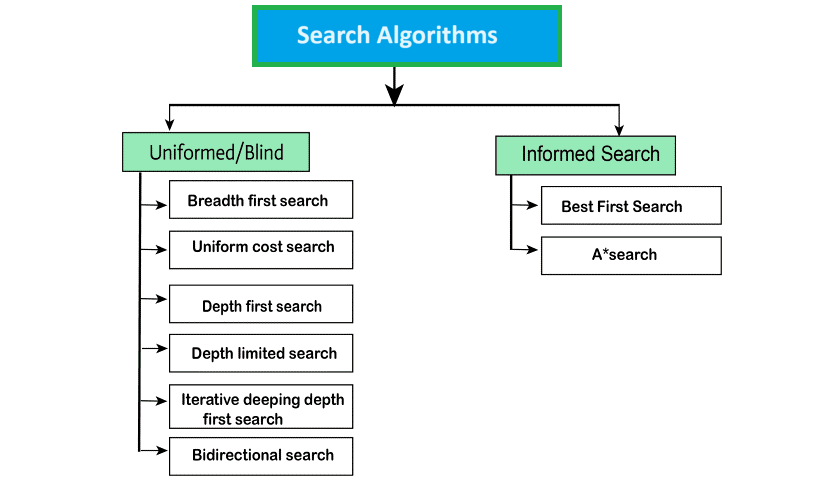
Types of search algorithm in Artificial Intelligence.

Uninformed / Blind Search:

Uninformed search lacks domain knowledge, such as information about the closeness or location of the goal. It employs a brute-force approach, focusing solely on how to traverse the tree and identify leaf and goal nodes. This method, also known as blind search, operates without any specific information about the search space, including the initial state, operators, and goal test. In uninformed search, every node in the search tree is examined until the goal node is reached.

It can be divided into five main types:

  • Breadth-first search
  • Uniform cost search
  • Depth-first search
  • Iterative deepening depth-first search
  • Bidirectional Search

Informed search algorithms leverage domain knowledge. This approach benefits from problem-specific information guiding the search process. Unlike uninformed search, informed search strategies can efficiently find solutions by utilizing available problem information. Informed search is commonly referred to as Heuristic search.

A heuristic is a guiding principle that, while not always guaranteeing the best solutions, ensures the discovery of a good solution within a reasonable time frame. This characteristic distinguishes heuristic search as an effective method for informed search strategies.

Informed search excels in solving complex problems that may pose challenges for other approaches. Its ability to incorporate domain knowledge makes it a powerful tool for tackling intricacies that might be insurmountable through alternative methods.

  1. Greedy Search
  2. A* Search