Linear Regression vs Logistic Regression in Machine Learning
In this page, we will learn Linear Regression vs Logistic Regression in Machine Learning, Linear Regression, Logistic Regression, Difference between Linear Regression and Logistic Regression.
The two most well-known Machine Learning Algorithms that fall
under the supervised learning technique are Linear Regression
and Logistic Regression. Because both algorithms are
supervised, they employ a labeled dataset to generate
predictions. The biggest distinction between them, though, is
how they are employed. Regression problems are solved using
Linear Regression, while classification problems are solved
using Logistic Regression. Below is a description of both
methods, as well as a comparison table.
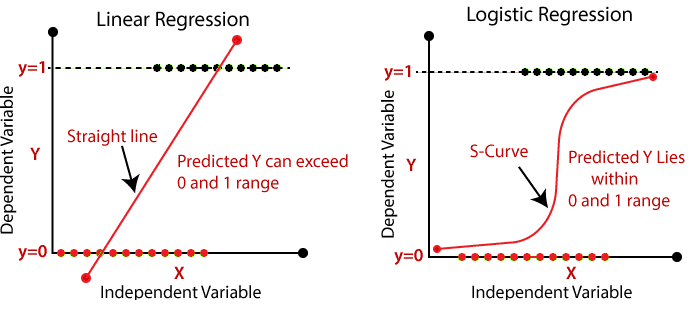
Linear Regression:
- Linear Regression is a simple machine learning algorithm that is used to solve regression problems and falls under the Supervised Learning technique.
- With the use of independent variables, it is used to predict a continuous dependent variable.
- The purpose of linear regression is to identify the best fit line for predicting the output of a continuous dependent variable.
- Simple Linear Regression is used when only one independent variable is used for prediction, while Multiple Linear Regression is used when more than two independent variables are utilized.
- The algorithm establishes the relationship between the dependent and independent variables by determining the best fit line. In addition, the relationship should be linear.
- Only continuous values such as price, age, wage, and so on should be the result of linear regression. The following diagram depicts the relationship between the dependent and independent variables:
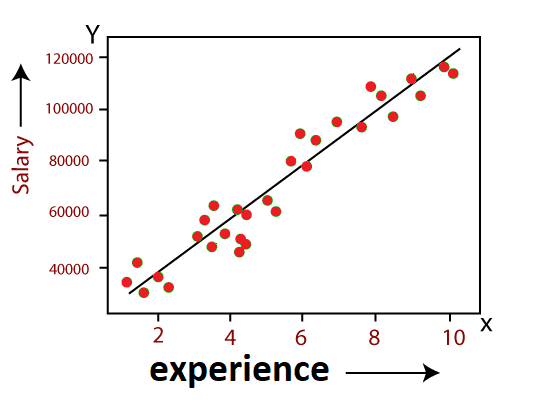
In above image the dependent variable is on Y-axis (salary)
and independent variable is on x-axis(experience). The
regression line can be written as:
y = a0 + a1x + ε
Where, a0 and a1 are the coefficients and ε is the error term.
Logistic Regression:
- Under Supervised Learning approaches, one of the most common Machine Learning algorithms is logistic regression.
- It can be used for both classification and regression problems, however it is more commonly employed for classification.
- With the help of independent factors, logistic regression is utilized to predict the categorical dependent variable.
- Only 0 and 1 can be the outcome of a Logistic Regression issue.
- When the probabilities between two classes must be calculated, logistic regression can be utilized. For example, if it will rain today or not, 0 or 1, true or false, and so on.
- The concept of Maximum Likelihood estimation underpins logistic regression. The observed data should, in this view, be the most likely.
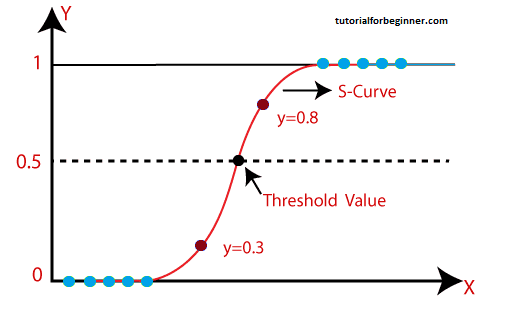
- We run the weighted sum of inputs through an activation function that can map values between 0 and 1 in logistic regression. The curve obtained is known as sigmoid curve or S-curve, and the activation function is known as sigmoid function. Consider the following illustration:
- The equation for logistic regression is:
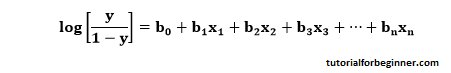
Difference between Linear Regression and Logistic Regression
| Linear Regression | Logistic Regression |
|---|---|
| Linear regression is a statistical technique for predicting a continuous dependent variable from a set of independent variables. | The categorical dependent variable is predicted using a set of independent variables using logistic regression. |
| Regression problems are solved using Linear Regression. | Classification difficulties are solved using logistic regression. |
| We predict the value of continuous variables using linear regression. | We predict the values of categorical variables using logistic regression. |
| In linear regression, we look for the best fit line, which allows us to predict the outcome with ease. | We find the S-curve in Logistic Regression and use it to classify the samples. |
| For accuracy estimation, the least square estimate approach is applied. | For accuracy estimation, the maximum likelihood estimation method is applied. |
| Linear Regression's output must be a continuous value, such as price or age. | Logistic Regression must produce a Categorical value, such as 0 or 1, Yes or No, and so on. |
| The relationship between the dependent variable and the independent variable must be linear in linear regression. | It is not necessary to have a linear relationship between the dependent and independent variables in logistic regression. |
| There is a possibility of collinearity between the independent variables in linear regression. | There should be no collinearity between the independent variables in logistic regression. |